104020 - 矩阵乘法
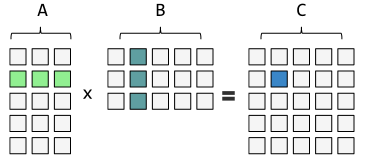
当第1个矩阵A的列数等于第2个矩阵B的行数时,这两个矩阵可以相乘,n×m的矩阵与 m×k的矩阵相乘变成n×k的矩阵,其乘积矩阵A×B的第i行第j列的元素为矩阵A第i行上的m个数与矩阵B第j列上的m个数对应相乘后所得的n个乘积之和。如图所示,C[1][1]=A[1][0]×B[0][1]+A[1][1]×B[1][1]+A[1][2]×B[2][1]。
例如:已知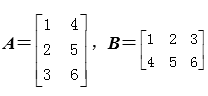 ,则乘积矩阵A×B的计算过程为:
,则乘积矩阵A×B的计算过程为:
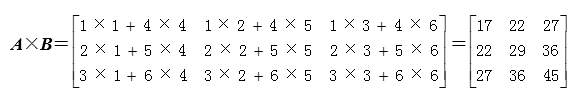
现输入一个n行m列的矩阵A和一个m行k列的矩阵B,输出A×B。
输入
第一行三个整数,分别为n,m,k。
随后输入A矩阵和B矩阵,矩阵中每个元素值的绝对值不超过1 000。
输出
输出A×B的矩阵,两数之间以空格间隔。
样例
输入
3 2 3 1 4 2 5 3 6 1 2 3 4 5 6
输出
17 22 27 22 29 36 27 36 45
