315003 - 选课

学院实行学分制，每门课程都有一定的学分，学员只要选修了这门课并考核通过就能获得相应的学分，学员最后的学分是他选修的各门课的学分的总和。

每个学员都要选择规定数量的课程。其中有些课程可以直接选修，有些课程需要一定的基础知识，必须在选了其他的一些课程的基础上才能选修。例如，《数据结构》必须在选修了《高级语言程序设计》之后才能选修。我们称《高级语言程序设计》是《数据结构》的先修课。每门课的直接先修课最多只有一门，两门课也可能存在相同的先修课。为便于表述每门课都有一个课号，课号依次为1,2,3,\cdots

例如下表中1是2的先修课，即如果要选修2，则1必定已被选过。同样，如果要选修3，那么1和2都一定已被选修过。

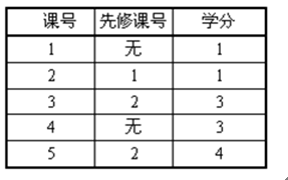
学员不可能学完学院所开设的所有课程，因此必须在入学时选定自己要学的课程。每个学员可选课程的总数是给定的。现在请你找出一种选课方案，使得你能得到学分最多，并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。

输入的第一行包括两个正整数M,N（中间用一个空格隔开）其中M表示待选课程总数（1≤M≤1000），N表示学员可以选的课程总数（1≤N≤M）。

以下M行每行代表一门课，课号依次为1,2,\cdots,M。每行有两个数（用一个空格隔开），第一个数为这门课的先修课的课号（若不存在先修课则该项为0），第二个数为这门课的学分。学分是不超过10的正整数。

输出文件第一行只有一个数，即实际所选课程的学分总数。以下N行，每行有一个数，表示学员所选课程的课号。