405020 - 神经网络

琪儿在研究神经网络，在她制作的简化模型中，神经网络是一张有向图，图中的结点称为神经元，而且两个神经元之间至多有一条边相连，图5.75是一个神经元的例子： 图5.75

图5.75中，X1~X3是信息输入渠道，Y1~Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。 神经元按一定的顺序排列，构成整个神经网络。在琪儿的模型之中，神经网络中的神经元分为输入层、输出层和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。图5.76是一个简单的三层神经网络的例子。 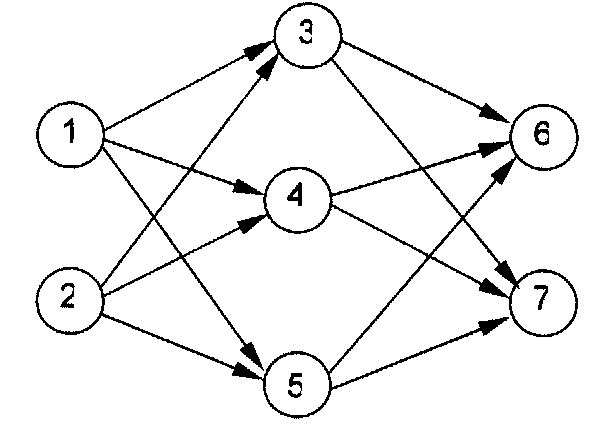图5.76

琪儿规定， Ci服从公式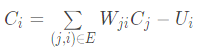： 公式中的 Wji（可能为负值）表示连接j号神经元和i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。 如此，在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。 现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

输入第一行是两个整数n（n是网络中所有神经元的数目，1≤n≤200）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。随后p行，每行有三个整数i，j和Wij，表示连接神经元i、j的边权值为Wij。

输出包含若干行，每行有两个整数，分别对应一个神经元的编号及其最后的状态。仅输出最后状态非零的输出层神经元状态，并且按照编号由小到大顺序输出。 若输出层的神经元最后状态均为0，则输出NULL。