513013 - 猫和老鼠

【题目描述】猫和老鼠（eat）

在一个魔法森林里，住着一只猫和一只老鼠。整个森林可以认为是一个无向图，图中有N个从1至N编号的景点，在景点之间有一些路连接。 一天，猫制造了一台GPS机器，它可以对老鼠准确的定位。 此时老鼠正在景点M（M≤N）处。以后的每个时间单位，老鼠都会选择去相邻的景点（可能有多个）中的一个或停留在原景点不动。而去这些地方所发生的概率是相等的。假设有P个景点与景点M相邻，它们分别是景点R、景点S，……景点Q，在时刻T老鼠处在景点M，则在（T＋1）时刻，老鼠有1/(1＋P) 的可能在景点R，有 1/(1＋P)的可能在景点 S，……，有1/(1＋P)的可能在景点Q，还有1/(1＋P)的可能停在景点M。 猫是很聪明的，所以，当她在景点C时，她会选一个更靠近老鼠的景点，如果这样的景点有多个，她会选一个标号最小的景点。由于猫太想吃掉老鼠了，如果走完第一步以后仍然没吃到老鼠，她还可以在本段时间内再向老鼠走近一步。 在每个时间单位，假设猫先走，老鼠后走。在某一时刻，若猫和老鼠位于同一个景点，则可怜的老鼠就被吃掉了。 试问在平均情况下，猫几步就可能吃到老鼠。

数据的第1行为两个整数N和E，以空格分隔，分别表示森林中的景点数和连接相邻景点的路的条数。对于 50%的数据，1≤N≤50。对于所有的数据，1≤N，E≤1000。 第2行包含两个整数C和M，以空格分隔，分别表示初始时猫和老鼠所在的景点的编号。 接下来E行，每行两个整数，第i＋2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。 所有的路都是无向的，即如果能从A走到B，就可以从B走到A。 输入保证任何两个景点之间不会有多于一条路直接相连，且猫和老鼠之间必有路直接或间接的相连。

输出1个实数，四舍五入保留三位小数，表示平均多少个时间单位后猫会把老鼠吃掉。

如图13.6所示，开始时，猫和老鼠分别在景点1和景点4。 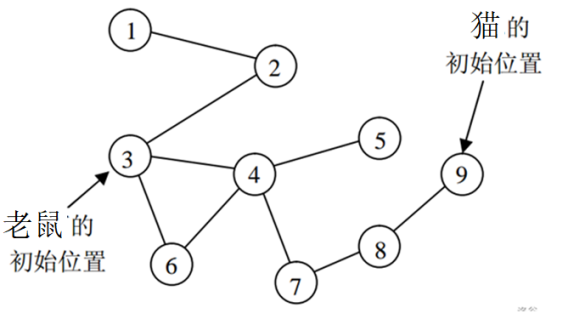图13.6

第一个时刻，猫先走，她向更靠近老鼠（景点4）的景点走动，走到景点2，然后走到景点3；假定忽略走路所花时间。 老鼠后走，有两种可能：第一种是走到景点3，这样猫和老鼠到达同一个景点，老鼠被吃掉，步数为1，概率为0.5。 第二种是停在景点 4，不被吃掉。概率为0.5。 到第二个时刻，猫向更靠近老鼠（景点4）的景点走动，只需要走一步即和老鼠在同一景点。因此这种情况下猫会在两步吃掉老鼠。 所以平均的步数是1×1/2＋2×1/2＝1.5 步。