只要努力飞翔，即使再弱小的蝴蝶也可以飞的很高
5020 - [COCI2018-2019#2] Sunčanje
lavko 做了一个不寻常的梦。在一个晴朗的早上，N 个白色的矩形一个接着一个爬上了 Slavko 家的屋顶，并在屋顶上晒太阳。每个矩形在屋顶都选定了一个位置，使得它的边与屋顶的棱角平行。有些矩形可能会覆盖在其它矩形所在的位置上。每个矩形的长、宽分别为 A_i,B_i，其与屋顶左方和下方的棱角的距离分别为 X_i,Y_i 。
日落后，矩形们从屋顶上下来，并睡了一觉。次日，它们发现，有些矩形变成了黄色，而有些仍为白色。变为黄色的矩形都是完全暴露在阳光下的。
请判断每个矩形是否变为了黄色。
Input
第一行输入正整数 N，表示矩形的个数。
接下来的 N 行，每行输入整数 X_i,Y_i,A_i,B_i。输入顺序与登上屋顶的顺序一致。
Output
输出 N 行。其中，若第 i 个矩形变为黄色，则在第 i 行输出 DA，否则在该行输出 NE。
Examples
Input
5 1 1 4 2 6 1 1 1 2 2 2 3 3 4 3 2 4 0 1 2
Output
NE DA NE DA DA
Input
3 3 3 1 1 2 2 3 3 1 1 5 5
Output
NE NE DA
Hint
【样例一解释】
矩形 1,3 没有完全暴露在阳光下，因而它们没有变为黄色：
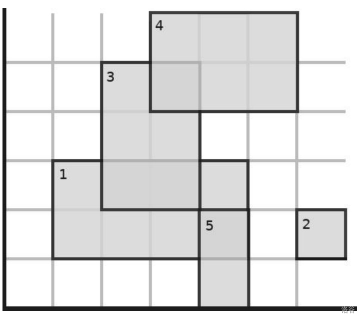
【数据范围】
对于 10\% 的数据，N \le 10^4。
对于 100\% 的数据，1 \le N \le 10^5，0 \le X_i,Y_i \le 10^9，1 \le A_i,B_i \le 10^9。